Take a triangular number, multiply it by 8 and add 1. What is special about your answer? Can you prove it?
Alison has been playing with numbers again. She started by choosing a triangular number, multiplied it by 8, and added 1. She noticed something interesting about her results…
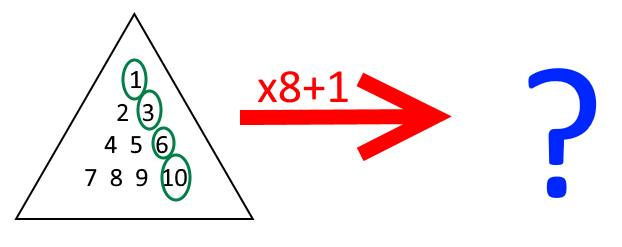
Try a few examples. Can you make a conjecture?
Once you’ve made a conjecture of your own, click below to see what Alison noticed:
“If T is a triangular number, 8T+1 is a square number.”
Can you prove the conjecture?
I wonder if there are any integers n where 8n+1 is a square number but n is not a triangular number…
Can you prove that if 8n+1 is a square number, n must be a triangular number?
Can you use your theorem to devise a quick way to check whether the following numbers are triangular numbers?
- 6214
- 3655
- 7626
- 8656
The title of this problem, “Iff”, is sometimes used by mathematicians as shorthand for “If and Only If”, which can also be represented by the double implication arrow ⟺. To explore the difference between “If”, “Only if” and “Iff”, try the problem Iffy Logic.
Age 14 to 18
