Can you explain the surprising results Jo found when she calculated the difference between square numbers?
This problem follows on from Hollow Squares and What’s Possible?.
Jo has been experimenting with pairs of two-digit numbers. She has been looking at the difference of their squares.
Jo has collected together some answers which she found quite surprising:
Can you find other pairs which give multiples of 1000? Do you notice anything special about these pairs of numbers?
Jo was also surprised to get these answers:
Can you find any other pairs which give repeated digits? Do you notice anything special about these pairs of numbers?
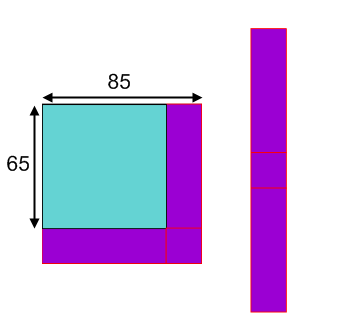
Jo wanted to explain why she was getting these surprising results. She drew some diagrams to help her. Here is the diagram she used to work out 85²−65²:
Now you should be able to work out these calculations without a calculator:
Can you write 1000,2000,3000… as the difference of two square numbers?
Can you write any of them in more than one way?
Can you write any repeated-digit number as the difference of two square numbers?
What about numbers like 434343, 123321, 123456…?
Is it possible to write every number as the difference of two square numbers?
This problem is also available in French: Plus ou Moins
Age 14 to 16