Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.
To work on this problem you may want to print out some dotty paper
When the dots on square dotty paper are joined by straight lines the enclosed figures have dots on their perimeter (p) and often internal (i) ones as well.
Figures can be described in this way: (p,i).
For example, the red square has a (p,i) of (4,0), the grey triangle (3,1), the green triangle (5,0) and the blue hexagon (6,4):
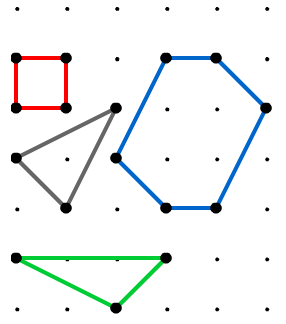
Each figure you produce will always enclose an area (A) of the square dotty paper.
The examples in the diagram have areas of 1, 112, and 6 sq units.
Check that you agree.
Draw more figures and keep a record of their perimeter points (p), interior points (i) and areas (A).
Can you find a relationship between these three variables?
Click here for a poster of this problem.
Age 14 to 16




